Algebra.Lattice.Wide

Documentation

data Wide a

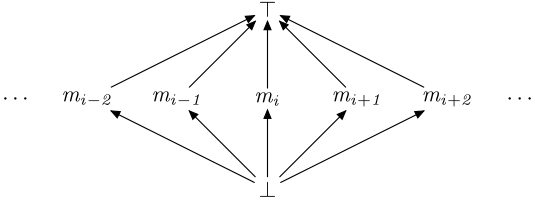
Graft a distinct top and bottom onto any type. The Top is identity for /\ and the absorbing element for \/. The Bottom is the identity for \/ and and the absorbing element for /\. Two Middle values join to top, unless they are equal.

Constructors

Top

Middle a

Bottom

Instances

Monad Wide

Defined in Algebra.Lattice.Wide

Methods

(>>=) :: Wide a -> (a -> Wide b) -> Wide b

(>>) :: Wide a -> Wide b -> Wide b

return :: a -> Wide a

fail :: String -> Wide a

Functor Wide

Defined in Algebra.Lattice.Wide

Methods

fmap :: (a -> b) -> Wide a -> Wide b

(<$) :: a -> Wide b -> Wide a

Applicative Wide

Defined in Algebra.Lattice.Wide

Methods

pure :: a -> Wide a

(<*>) :: Wide (a -> b) -> Wide a -> Wide b

liftA2 :: (a -> b -> c) -> Wide a -> Wide b -> Wide c

(*>) :: Wide a -> Wide b -> Wide b

(<*) :: Wide a -> Wide b -> Wide a

Foldable Wide

Defined in Algebra.Lattice.Wide

Methods

fold :: Monoid m => Wide m -> m

foldMap :: Monoid m => (a -> m) -> Wide a -> m

foldr :: (a -> b -> b) -> b -> Wide a -> b

foldr' :: (a -> b -> b) -> b -> Wide a -> b

foldl :: (b -> a -> b) -> b -> Wide a -> b

foldl' :: (b -> a -> b) -> b -> Wide a -> b

foldr1 :: (a -> a -> a) -> Wide a -> a

foldl1 :: (a -> a -> a) -> Wide a -> a

toList :: Wide a -> [a]

null :: Wide a -> Bool

length :: Wide a -> Int

elem :: Eq a => a -> Wide a -> Bool

maximum :: Ord a => Wide a -> a

minimum :: Ord a => Wide a -> a

sum :: Num a => Wide a -> a

product :: Num a => Wide a -> a

Traversable Wide

Defined in Algebra.Lattice.Wide

Methods

traverse :: Applicative f => (a -> f b) -> Wide a -> f (Wide b)

sequenceA :: Applicative f => Wide (f a) -> f (Wide a)

mapM :: Monad m => (a -> m b) -> Wide a -> m (Wide b)

sequence :: Monad m => Wide (m a) -> m (Wide a)

Eq a => Eq (Wide a)

Defined in Algebra.Lattice.Wide

Methods

(==) :: Wide a -> Wide a -> Bool

(/=) :: Wide a -> Wide a -> Bool

Data a => Data (Wide a)

Defined in Algebra.Lattice.Wide

Methods

gfoldl :: (forall d b. Data d => c (d -> b) -> d -> c b) -> (forall g. g -> c g) -> Wide a -> c (Wide a)

gunfold :: (forall b r. Data b => c (b -> r) -> c r) -> (forall r. r -> c r) -> Constr -> c (Wide a)

toConstr :: Wide a -> Constr

dataTypeOf :: Wide a -> DataType

dataCast1 :: Typeable t => (forall d. Data d => c (t d)) -> Maybe (c (Wide a))

dataCast2 :: Typeable t => (forall d e. (Data d, Data e) => c (t d e)) -> Maybe (c (Wide a))

gmapT :: (forall b. Data b => b -> b) -> Wide a -> Wide a

gmapQl :: (r -> r' -> r) -> r -> (forall d. Data d => d -> r') -> Wide a -> r

gmapQr :: (r' -> r -> r) -> r -> (forall d. Data d => d -> r') -> Wide a -> r

gmapQ :: (forall d. Data d => d -> u) -> Wide a -> [u]

gmapQi :: Int -> (forall d. Data d => d -> u) -> Wide a -> u

gmapM :: Monad m => (forall d. Data d => d -> m d) -> Wide a -> m (Wide a)

gmapMp :: MonadPlus m => (forall d. Data d => d -> m d) -> Wide a -> m (Wide a)

gmapMo :: MonadPlus m => (forall d. Data d => d -> m d) -> Wide a -> m (Wide a)

Ord a => Ord (Wide a)

Defined in Algebra.Lattice.Wide

Methods

compare :: Wide a -> Wide a -> Ordering

(<) :: Wide a -> Wide a -> Bool

(<=) :: Wide a -> Wide a -> Bool

(>) :: Wide a -> Wide a -> Bool

(>=) :: Wide a -> Wide a -> Bool

max :: Wide a -> Wide a -> Wide a

min :: Wide a -> Wide a -> Wide a

Read a => Read (Wide a)

Defined in Algebra.Lattice.Wide

Methods

readsPrec :: Int -> ReadS (Wide a)

readList :: ReadS [Wide a]

readPrec :: ReadPrec (Wide a)

readListPrec :: ReadPrec [Wide a]

Show a => Show (Wide a)

Defined in Algebra.Lattice.Wide

Methods

showsPrec :: Int -> Wide a -> ShowS

show :: Wide a -> String

showList :: [Wide a] -> ShowS

Generic (Wide a)

Defined in Algebra.Lattice.Wide

Associated Types

type Rep (Wide a) :: Type -> Type

Methods

from :: Wide a -> Rep (Wide a) x

to :: Rep (Wide a) x -> Wide a

Function a => Function (Wide a)

Defined in Algebra.Lattice.Wide

Methods

function :: (Wide a -> b) -> Wide a :-> b

Arbitrary a => Arbitrary (Wide a)

Defined in Algebra.Lattice.Wide

Methods

arbitrary :: Gen (Wide a)

shrink :: Wide a -> [Wide a]

CoArbitrary a => CoArbitrary (Wide a)

Defined in Algebra.Lattice.Wide

Methods

coarbitrary :: Wide a -> Gen b -> Gen b

NFData a => NFData (Wide a)

Defined in Algebra.Lattice.Wide

Methods

rnf :: Wide a -> ()

Hashable a => Hashable (Wide a)

Defined in Algebra.Lattice.Wide

Methods

hashWithSalt :: Int -> Wide a -> Int

hash :: Wide a -> Int

Universe a => Universe (Wide a)

Defined in Algebra.Lattice.Wide

Methods

universe :: [Wide a]

Finite a => Finite (Wide a)

Defined in Algebra.Lattice.Wide

Methods

universeF :: [Wide a]

cardinality :: Tagged (Wide a) Natural

Eq a => PartialOrd (Wide a)

Defined in Algebra.Lattice.Wide

Methods

leq :: Wide a -> Wide a -> Bool

comparable :: Wide a -> Wide a -> Bool

Eq a => BoundedMeetSemiLattice (Wide a)

Defined in Algebra.Lattice.Wide

Methods

top :: Wide a

Eq a => BoundedJoinSemiLattice (Wide a)

Defined in Algebra.Lattice.Wide

Methods

bottom :: Wide a

Eq a => Lattice (Wide a)

Defined in Algebra.Lattice.Wide

Methods

(\/) :: Wide a -> Wide a -> Wide a

(/\) :: Wide a -> Wide a -> Wide a

Generic1 Wide

Defined in Algebra.Lattice.Wide

Associated Types

type Rep1 Wide :: k -> Type

Methods

from1 :: Wide a -> Rep1 Wide a

to1 :: Rep1 Wide a -> Wide a

type Rep (Wide a)

Defined in Algebra.Lattice.Wide

type Rep (Wide a) = D1 (MetaData "Wide" "Algebra.Lattice.Wide" "lattices-2.0.2-HdMTcqWeXqlAAQvdNaFFrQ" False) (C1 (MetaCons "Top" PrefixI False) (U1 :: Type -> Type) :+: (C1 (MetaCons "Middle" PrefixI False) (S1 (MetaSel (Nothing :: Maybe Symbol) NoSourceUnpackedness NoSourceStrictness DecidedLazy) (Rec0 a)) :+: C1 (MetaCons "Bottom" PrefixI False) (U1 :: Type -> Type)))

type Rep1 Wide

Defined in Algebra.Lattice.Wide

type Rep1 Wide = D1 (MetaData "Wide" "Algebra.Lattice.Wide" "lattices-2.0.2-HdMTcqWeXqlAAQvdNaFFrQ" False) (C1 (MetaCons "Top" PrefixI False) (U1 :: Type -> Type) :+: (C1 (MetaCons "Middle" PrefixI False) (S1 (MetaSel (Nothing :: Maybe Symbol) NoSourceUnpackedness NoSourceStrictness DecidedLazy) Par1) :+: C1 (MetaCons "Bottom" PrefixI False) (U1 :: Type -> Type)))