| Safe Haskell | None |
|---|
Quantum.Synthesis.Clifford
Description
This module provides an efficient symbolic representation of the Clifford group on one qubit. This group is generated by S, H, and the scalar ω = eiπ/4. It has 192 elements.
- data Clifford
- clifford_X :: Clifford
- clifford_Y :: Clifford
- clifford_Z :: Clifford
- clifford_H :: Clifford
- clifford_S :: Clifford
- clifford_SH :: Clifford
- clifford_E :: Clifford
- clifford_W :: Clifford
- class ToClifford a where
- to_clifford :: a -> Clifford
- clifford_decompose :: ToClifford a => a -> (Int, Int, Int, Int)
- data Axis
- clifford_decompose_coset :: ToClifford a => a -> (Axis, Int, Int, Int)
- clifford_id :: Clifford
- clifford_mult :: Clifford -> Clifford -> Clifford
- clifford_inv :: ToClifford a => a -> Clifford
- clifford_tconj :: Clifford -> (Axis, Clifford)
The Clifford group
A type representing single-qubit Clifford operators.
Constructors
The Pauli X-gate as a Clifford operator.
The Pauli Y-gate as a Clifford operator.
The Pauli Z-gate as a Clifford operator.
The Hadamard gate as a Clifford operator.
The Clifford operator S.
The Clifford operator SH.
The Clifford operator E = HS3ω3. This operator is uniquely determined by the properties E³ = I, EXE⁻¹ = Y, EYE⁻¹ = Z, and EZE⁻¹ = X.
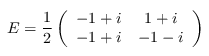
The Clifford operator ω = eiπ/4.
class ToClifford a whereSource
A type class for things that can be exactly converted to a
Clifford operator. One particular instance of this is String, so
that Clifford operators can be denoted, e.g.,
to_clifford "-iX"
The valid characters for such string conversions are "XYZHSEIWi-".
Instances
| ToClifford Char | |
| ToClifford Axis | |
| ToClifford Clifford | |
| ToClifford a => ToClifford [a] | |
| (Ring a, Eq a, Adjoint a) => ToClifford (SO3 a) |
Deconstructors
clifford_decompose :: ToClifford a => a -> (Int, Int, Int, Int)Source
Given a Clifford operator U, return (a, b, c, d) such that
- U = EaXbScωd,
- a ∈ {0, 1, 2}, b ∈ {0, 1}, c ∈ {0, …, 3}, and d ∈ {0, …, 7}.
Here, E = HS3ω3. Note that E, X, S, and ω have order 3, 2, 4, and 8, respectively. Moreover, each Clifford operator can be uniquely represented as above.
A axis is either I, H, or SH.
clifford_decompose_coset :: ToClifford a => a -> (Axis, Int, Int, Int)Source
Given a Clifford operator U, return (K, b, c, d) such that
- U = KXbScωd,
- K ∈ {I, H, SH}, b ∈ {0, 1}, c ∈ {0, …, 3}, and d ∈ {0, …, 7}.
Group operations
The identity Clifford operator.
clifford_mult :: Clifford -> Clifford -> CliffordSource
Clifford multiplication.
clifford_inv :: ToClifford a => a -> CliffordSource
Clifford inverse.
Conjugation by T
clifford_tconj :: Clifford -> (Axis, Clifford)Source
Given a Clifford gate C, return an axis K ∈ {I, H, SH} and a Clifford gate C' such that
- CT = KTC'.