Optics.Lens

A Lens is a generalised or first-class field.

If we have a value s :: S, and a l :: Lens' S A, we can get the "field value" of type A using view l s. We can also update (or put or set) the value using over (or set).

For example, given the following definitions:

>>> data Human = Human { _name :: String, _location :: String } deriving Show
>>> let human = Human "Bob" "London"

we can make a Lens for _name field:

>>> let name = lens _name $ \s x -> s { _name = x }

which we can use as a Getter:

>>> view name human
"Bob"

or a Setter:

>>> set name "Robert" human
Human {_name = "Robert", _location = "London"}

Formation

type Lens s t a b = Optic A_Lens NoIx s t a b

Type synonym for a type-modifying lens.

type Lens' s a = Optic' A_Lens NoIx s a

Type synonym for a type-preserving lens.

Introduction

lens :: (s -> a) -> (s -> b -> t) -> Lens s t a b

Build a lens from a getter and a setter, which must respect the well-formedness laws.

If you want to build a Lens from the van Laarhoven representation, use lensVL.

Elimination

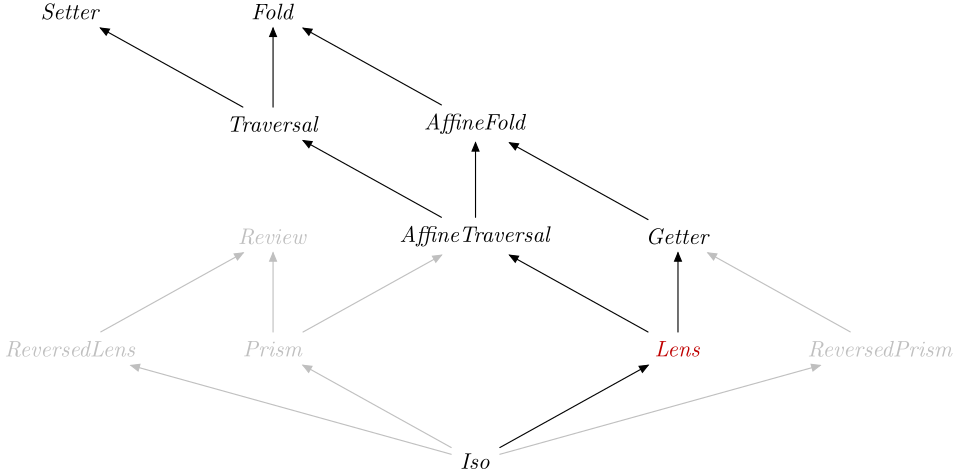
A Lens is in particular a Getter and a Setter, therefore you can specialise types to obtain:

view :: Lens s t a b -> s -> a

over :: Lens s t a b -> (a -> b) -> s -> t
set  :: Lens s t a b ->       b  -> s -> t

Computation

view (lens f g)   s ≡ f s
set  (lens f g) a s ≡ g s a

Well-formedness

• GetPut: You get back what you put in:

  view l (set l v s) ≡ v
  

• PutGet: Putting back what you got doesn’t change anything:

  set l (view l s) s ≡ s
  

• PutPut: Setting twice is the same as setting once:

  set l v' (set l v s) ≡ set l v' s
  

Additional introduction forms

See Data.Tuple.Optics for Lenses for tuples.

equality' :: Lens a b a b

Strict version of equality.

Useful for strictifying optics with lazy (irrefutable) pattern matching by precomposition, e.g.

_1' = equality' % _1

chosen :: Lens (Either a a) (Either b b) a b

Focus on both sides of an Either.

alongside :: (Is k A_Lens, Is l A_Lens) => Optic k is s t a b -> Optic l js s' t' a' b' -> Lens (s, s') (t, t') (a, a') (b, b')

Make a Lens from two other lenses by executing them on their respective halves of a product.

>>> (Left 'a', Right 'b') ^. alongside chosen chosen
('a','b')

>>> (Left 'a', Right 'b') & alongside chosen chosen .~ ('c','d')
(Left 'c',Right 'd')

united :: Lens' a ()

We can always retrieve a () from any type.

>>> view united "hello"
()

>>> set united () "hello"
"hello"

Additional elimination forms

withLens :: Is k A_Lens => Optic k is s t a b -> ((s -> a) -> (s -> b -> t) -> r) -> r

Work with a lens as a getter and a setter.

withLens (lens f g) k ≡ k f g

Subtyping

data A_Lens

Tag for a lens.

Instances

ReversibleOptic A_Lens

Defined in Optics.Re

Associated Types

type ReversedOptic A_Lens = (r :: Type)

Methods

re :: AcceptsEmptyIndices "re" is => Optic A_Lens is s t a b -> Optic (ReversedOptic A_Lens) is b a t s

Is A_Lens A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens A_Fold p -> (Constraints A_Lens p -> r) -> Constraints A_Fold p -> r

Is A_Lens An_AffineFold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens An_AffineFold p -> (Constraints A_Lens p -> r) -> Constraints An_AffineFold p -> r

Is A_Lens A_Getter

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens A_Getter p -> (Constraints A_Lens p -> r) -> Constraints A_Getter p -> r

Is A_Lens A_Setter

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens A_Setter p -> (Constraints A_Lens p -> r) -> Constraints A_Setter p -> r

Is A_Lens A_Traversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens A_Traversal p -> (Constraints A_Lens p -> r) -> Constraints A_Traversal p -> r

Is A_Lens An_AffineTraversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Lens An_AffineTraversal p -> (Constraints A_Lens p -> r) -> Constraints An_AffineTraversal p -> r

Is An_Iso A_Lens

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Lens p -> (Constraints An_Iso p -> r) -> Constraints A_Lens p -> r

Arrow arr => ArrowOptic A_Lens arr

Defined in Optics.Arrow

Methods

overA :: Optic A_Lens is s t a b -> arr a b -> arr s t

ToReadOnly A_Lens s t a b

Defined in Optics.ReadOnly

Methods

getting :: Optic A_Lens is s t a b -> Optic' (Join A_Getter A_Lens) is s a

IxOptic A_Lens s t a b

Defined in Optics.Indexed.Core

Methods

noIx :: NonEmptyIndices is => Optic A_Lens is s t a b -> Optic A_Lens NoIx s t a b

type ReversedOptic A_Lens

Defined in Optics.Re

type ReversedOptic A_Lens = A_ReversedLens

van Laarhoven encoding

The van Laarhoven encoding of lenses is isomorphic to the profunctor encoding used internally by optics, but converting back and forth may have a performance penalty.

type LensVL s t a b = forall f. Functor f => (a -> f b) -> s -> f t

Type synonym for a type-modifying van Laarhoven lens.

type LensVL' s a = LensVL s s a a

Type synonym for a type-preserving van Laarhoven lens.

lensVL :: LensVL s t a b -> Lens s t a b

Build a lens from the van Laarhoven representation.

toLensVL :: Is k A_Lens => Optic k is s t a b -> LensVL s t a b

Convert a lens to the van Laarhoven representation.

withLensVL :: Is k A_Lens => Optic k is s t a b -> (LensVL s t a b -> r) -> r

Work with a lens in the van Laarhoven representation.