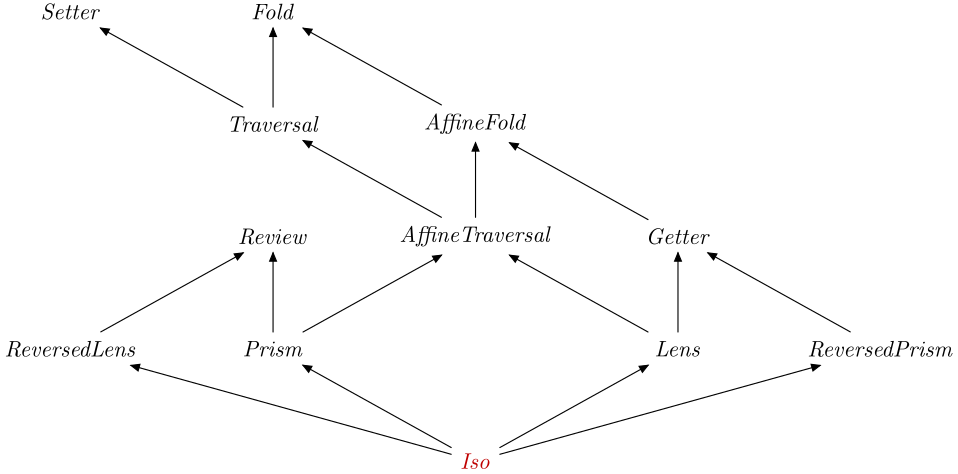
Optics.Iso

An Isomorphism expresses the fact that two types have the same structure, and hence can be converted from one to the other in either direction.

Formation

type Iso s t a b = Optic An_Iso NoIx s t a b

Type synonym for a type-modifying iso.

type Iso' s a = Optic' An_Iso NoIx s a

Type synonym for a type-preserving iso.

Introduction

iso :: (s -> a) -> (b -> t) -> Iso s t a b

Build an iso from a pair of inverse functions.

If you want to build an Iso from the van Laarhoven representation, use isoVL from the optics-vl package.

Elimination

An Iso is in particular a Getter, a Review and a Setter, therefore you can specialise types to obtain:

view   :: Iso' s a -> s -> a
review :: Iso' s a -> a -> s

over   :: Iso s t a b -> (a -> b) -> s -> t
set    :: Iso s t a b ->       b  -> s -> t

If you want to view a type-modifying Iso that is insufficiently polymorphic to be used as a type-preserving Iso', use getting:

view . getting :: Iso s t a b -> s -> a

Computation

view   (iso f g) ≡ f
review (iso f g) ≡ g

Well-formedness

The functions translating back and forth must be mutually inverse:

view i . review i ≡ id
review i . view i ≡ id

Additional introduction forms

equality :: (s ~ a, t ~ b) => Iso s t a b

Capture type constraints as an isomorphism.

Note: This is the identity optic:

>>> :t view equality
view equality :: a -> a

simple :: Iso' a a

Proof of reflexivity.

coerced :: (Coercible s a, Coercible t b) => Iso s t a b

Data types that are representationally equal are isomorphic.

>>> view coerced 'x' :: Identity Char
Identity 'x'

coercedTo :: forall a s. Coercible s a => Iso' s a

Type-preserving version of coerced with type parameters rearranged for TypeApplications.

>>> newtype MkInt = MkInt Int deriving Show

>>> over (coercedTo @Int) (*3) (MkInt 2)
MkInt 6

coerced1 :: forall f s a. (Coercible s (f s), Coercible a (f a)) => Iso (f s) (f a) s a

Special case of coerced for trivial newtype wrappers.

>>> over (coerced1 @Identity) (++ "bar") (Identity "foo")
Identity "foobar"

non :: Eq a => a -> Iso' (Maybe a) a

If v is an element of a type a, and a' is a sans the element v, then non v is an isomorphism from Maybe a' to a.

non ≡ non' . only

Keep in mind this is only a real isomorphism if you treat the domain as being Maybe (a sans v).

This is practically quite useful when you want to have a Map where all the entries should have non-zero values.

>>> Map.fromList [("hello",1)] & at "hello" % non 0 %~ (+2)
fromList [("hello",3)]

>>> Map.fromList [("hello",1)] & at "hello" % non 0 %~ (subtract 1)
fromList []

>>> Map.fromList [("hello",1)] ^. at "hello" % non 0
1

>>> Map.fromList [] ^. at "hello" % non 0
0

This combinator is also particularly useful when working with nested maps.

e.g. When you want to create the nested Map when it is missing:

>>> Map.empty & at "hello" % non Map.empty % at "world" ?~ "!!!"
fromList [("hello",fromList [("world","!!!")])]

and when have deleting the last entry from the nested Map mean that we should delete its entry from the surrounding one:

>>> Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % non Map.empty % at "world" .~ Nothing
fromList []

It can also be used in reverse to exclude a given value:

>>> non 0 # rem 10 4
Just 2

>>> non 0 # rem 10 5
Nothing

Since: 0.2

non' :: Prism' a () -> Iso' (Maybe a) a

non' p generalizes non (p # ()) to take any unit Prism

This function generates an isomorphism between Maybe (a | isn't p a) and a.

>>> Map.singleton "hello" Map.empty & at "hello" % non' _Empty % at "world" ?~ "!!!"
fromList [("hello",fromList [("world","!!!")])]

>>> Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % non' _Empty % at "world" .~ Nothing
fromList []

Since: 0.2

anon :: a -> (a -> Bool) -> Iso' (Maybe a) a

anon a p generalizes non a to take any value and a predicate.

anon a ≡ non' . nearly a

This function assumes that p a holds True and generates an isomorphism between Maybe (a | not (p a)) and a.

>>> Map.empty & at "hello" % anon Map.empty Map.null % at "world" ?~ "!!!"
fromList [("hello",fromList [("world","!!!")])]

>>> Map.fromList [("hello", Map.fromList [("world","!!!")])] & at "hello" % anon Map.empty Map.null % at "world" .~ Nothing
fromList []

Since: 0.2

curried :: Iso ((a, b) -> c) ((d, e) -> f) (a -> b -> c) (d -> e -> f)

The canonical isomorphism for currying and uncurrying a function.

curried = iso curry uncurry

>>> view curried fst 3 4
3

uncurried :: Iso (a -> b -> c) (d -> e -> f) ((a, b) -> c) ((d, e) -> f)

The canonical isomorphism for uncurrying and currying a function.

uncurried = iso uncurry curry

uncurried = re curried

>>> (view uncurried (+)) (1,2)
3

flipped :: Iso (a -> b -> c) (a' -> b' -> c') (b -> a -> c) (b' -> a' -> c')

The isomorphism for flipping a function.

>>> (view flipped (,)) 1 2
(2,1)

involuted :: (a -> a) -> Iso' a a

Given a function that is its own inverse, this gives you an Iso using it in both directions.

involuted ≡ join iso

>>> "live" ^. involuted reverse
"evil"

>>> "live" & involuted reverse %~ ('d':)
"lived"

class Bifunctor p => Swapped p where

This class provides for symmetric bifunctors.

Methods

swapped :: Iso (p a b) (p c d) (p b a) (p d c)

swapped . swapped ≡ id
first f . swapped = swapped . second f
second g . swapped = swapped . first g
bimap f g . swapped = swapped . bimap g f

>>> view swapped (1,2)
(2,1)

Instances

Swapped Either

Defined in Optics.Iso

Methods

swapped :: Iso (Either a b) (Either c d) (Either b a) (Either d c)

Swapped (,)

Defined in Optics.Iso

Methods

swapped :: Iso (a, b) (c, d) (b, a) (d, c)

Additional elimination forms

withIso :: Iso s t a b -> ((s -> a) -> (b -> t) -> r) -> r

Extract the two components of an isomorphism.

au :: Functor f => Iso s t a b -> ((b -> t) -> f s) -> f a

Based on ala from Conor McBride's work on Epigram.

This version is generalized to accept any Iso, not just a newtype.

>>> au (coerced1 @Sum) foldMap [1,2,3,4]
10

You may want to think of this combinator as having the following, simpler type:

au :: Iso s t a b -> ((b -> t) -> e -> s) -> e -> a

under :: Iso s t a b -> (t -> s) -> b -> a

The opposite of working over a Setter is working under an isomorphism.

under ≡ over . re

Combinators

The re combinator can be used to reverse an Iso:

re :: Iso s t a b -> Iso b a t s

mapping :: (Functor f, Functor g) => Iso s t a b -> Iso (f s) (g t) (f a) (g b)

This can be used to lift any Iso into an arbitrary Functor.

Subtyping

data An_Iso :: OpticKind

Tag for an iso.

Instances

ReversibleOptic An_Iso

Defined in Optics.Re

Associated Types

type ReversedOptic An_Iso = (r :: Type)

Methods

re :: AcceptsEmptyIndices "re" is => Optic An_Iso is s t a b -> Optic (ReversedOptic An_Iso) is b a t s

Is An_Iso A_Review

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Review p -> (Constraints An_Iso p -> r) -> Constraints A_Review p -> r

Is An_Iso A_ReversedLens

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_ReversedLens p -> (Constraints An_Iso p -> r) -> Constraints A_ReversedLens p -> r

Is An_Iso A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Fold p -> (Constraints An_Iso p -> r) -> Constraints A_Fold p -> r

Is An_Iso An_AffineFold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso An_AffineFold p -> (Constraints An_Iso p -> r) -> Constraints An_AffineFold p -> r

Is An_Iso A_Getter

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Getter p -> (Constraints An_Iso p -> r) -> Constraints A_Getter p -> r

Is An_Iso A_ReversedPrism

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_ReversedPrism p -> (Constraints An_Iso p -> r) -> Constraints A_ReversedPrism p -> r

Is An_Iso A_Setter

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Setter p -> (Constraints An_Iso p -> r) -> Constraints A_Setter p -> r

Is An_Iso A_Traversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Traversal p -> (Constraints An_Iso p -> r) -> Constraints A_Traversal p -> r

Is An_Iso An_AffineTraversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso An_AffineTraversal p -> (Constraints An_Iso p -> r) -> Constraints An_AffineTraversal p -> r

Is An_Iso A_Prism

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Prism p -> (Constraints An_Iso p -> r) -> Constraints A_Prism p -> r

Is An_Iso A_Lens

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Lens p -> (Constraints An_Iso p -> r) -> Constraints A_Lens p -> r

Arrow arr => ArrowOptic An_Iso arr

Defined in Optics.Arrow

Methods

overA :: Optic An_Iso is s t a b -> arr a b -> arr s t

ToReadOnly An_Iso s t a b

Defined in Optics.ReadOnly

Methods

getting :: Optic An_Iso is s t a b -> Optic' (Join A_Getter An_Iso) is s a

type ReversedOptic An_Iso

Defined in Optics.Re

type ReversedOptic An_Iso = An_Iso