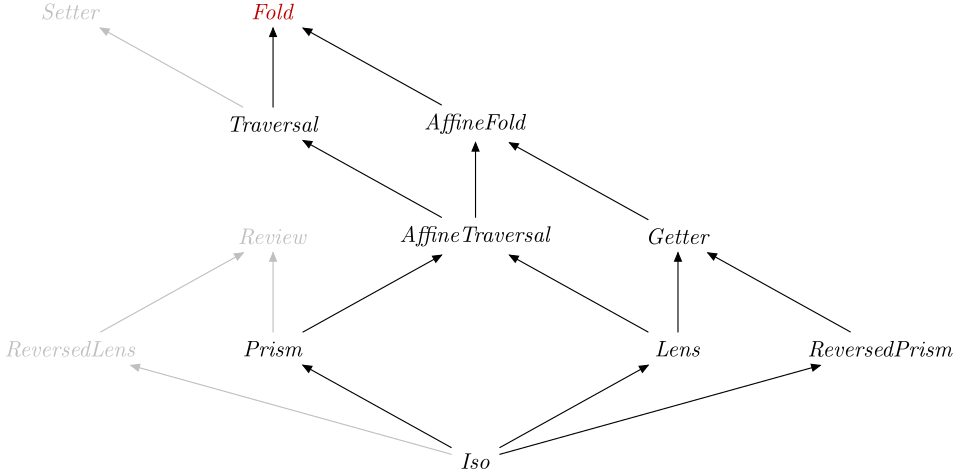
Optics.Fold

A Fold S A has the ability to extract some number of elements of type A from a container of type S. For example, toListOf can be used to obtain the contained elements as a list. Unlike a Traversal, there is no way to set or update elements.

This can be seen as a generalisation of traverse_, where the type S does not need to be a type constructor with A as the last parameter.

A close relative is the AffineFold, which is a Fold that contains at most one element.

Formation

type Fold s a = Optic' A_Fold NoIx s a

Type synonym for a fold.

Introduction

foldVL :: (forall f. Applicative f => (a -> f u) -> s -> f v) -> Fold s a

Obtain a Fold by lifting traverse_ like function.

foldVL . traverseOf_ ≡ id
traverseOf_ . foldVL ≡ id

Elimination

foldOf :: (Is k A_Fold, Monoid a) => Optic' k is s a -> s -> a

Combine the results of a fold using a monoid.

foldMapOf :: (Is k A_Fold, Monoid m) => Optic' k is s a -> (a -> m) -> s -> m

Fold via embedding into a monoid.

foldrOf :: Is k A_Fold => Optic' k is s a -> (a -> r -> r) -> r -> s -> r

Fold right-associatively.

foldlOf' :: Is k A_Fold => Optic' k is s a -> (r -> a -> r) -> r -> s -> r

Fold left-associatively, and strictly.

toListOf :: Is k A_Fold => Optic' k is s a -> s -> [a]

Fold to a list.

>>> toListOf (_1 % folded % _Right) ([Right 'h', Left 5, Right 'i'], "bye")
"hi"

sequenceOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s (f a) -> s -> f ()

Evaluate each action in a structure observed by a Fold from left to right, ignoring the results.

sequenceA_ ≡ sequenceOf_ folded

>>> sequenceOf_ each (putStrLn "hello",putStrLn "world")
hello
world

traverseOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> (a -> f r) -> s -> f ()

Traverse over all of the targets of a Fold, computing an Applicative-based answer, but unlike traverseOf do not construct a new structure. traverseOf_ generalizes traverse_ to work over any Fold.

>>> traverseOf_ each putStrLn ("hello","world")
hello
world

traverse_ ≡ traverseOf_ folded

forOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> s -> (a -> f r) -> f ()

A version of traverseOf_ with the arguments flipped.

Computation

traverseOf_ (foldVL f) ≡ f

Additional introduction forms

folded :: Foldable f => Fold (f a) a

Fold via the Foldable class.

folding :: Foldable f => (s -> f a) -> Fold s a

Obtain a Fold by lifting an operation that returns a Foldable result.

This can be useful to lift operations from Data.List and elsewhere into a Fold.

>>> toListOf (folding tail) [1,2,3,4]
[2,3,4]

foldring :: (forall f. Applicative f => (a -> f u -> f u) -> f v -> s -> f w) -> Fold s a

Obtain a Fold by lifting foldr like function.

>>> toListOf (foldring foldr) [1,2,3,4]
[1,2,3,4]

unfolded :: (s -> Maybe (a, s)) -> Fold s a

Build a Fold that unfolds its values from a seed.

unfoldr ≡ toListOf . unfolded

>>> toListOf (unfolded $ \b -> if b == 0 then Nothing else Just (b, b - 1)) 10
[10,9,8,7,6,5,4,3,2,1]

Additional elimination forms

See also setOf, which constructs a Set from a Fold.

has :: Is k A_Fold => Optic' k is s a -> s -> Bool

Check to see if this optic matches 1 or more entries.

>>> has _Left (Left 12)
True

>>> has _Right (Left 12)
False

This will always return True for a Lens or Getter.

>>> has _1 ("hello","world")
True

hasn't :: Is k A_Fold => Optic' k is s a -> s -> Bool

Check to see if this Fold or Traversal has no matches.

>>> hasn't _Left (Right 12)
True

>>> hasn't _Left (Left 12)
False

headOf :: Is k A_Fold => Optic' k is s a -> s -> Maybe a

Retrieve the first entry of a Fold.

>>> headOf folded [1..10]
Just 1

>>> headOf each (1,2)
Just 1

lastOf :: Is k A_Fold => Optic' k is s a -> s -> Maybe a

Retrieve the last entry of a Fold.

>>> lastOf folded [1..10]
Just 10

>>> lastOf each (1,2)
Just 2

andOf :: Is k A_Fold => Optic' k is s Bool -> s -> Bool

Returns True if every target of a Fold is True.

>>> andOf each (True, False)
False
>>> andOf each (True, True)
True

and ≡ andOf folded

orOf :: Is k A_Fold => Optic' k is s Bool -> s -> Bool

Returns True if any target of a Fold is True.

>>> orOf each (True, False)
True
>>> orOf each (False, False)
False

or ≡ orOf folded

allOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool

Returns True if every target of a Fold satisfies a predicate.

>>> allOf each (>=3) (4,5)
True
>>> allOf folded (>=2) [1..10]
False

all ≡ allOf folded

anyOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool

Returns True if any target of a Fold satisfies a predicate.

>>> anyOf each (=='x') ('x','y')
True

noneOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool

Returns True only if no targets of a Fold satisfy a predicate.

>>> noneOf each (not . isn't _Nothing) (Just 3, Just 4, Just 5)
True
>>> noneOf (folded % folded) (<10) [[13,99,20],[3,71,42]]
False

productOf :: (Is k A_Fold, Num a) => Optic' k is s a -> s -> a

Calculate the Product of every number targeted by a Fold.

>>> productOf each (4,5)
20
>>> productOf folded [1,2,3,4,5]
120

product ≡ productOf folded

This operation may be more strict than you would expect. If you want a lazier version use \o -> getProduct . foldMapOf o Product.

sumOf :: (Is k A_Fold, Num a) => Optic' k is s a -> s -> a

Calculate the Sum of every number targeted by a Fold.

>>> sumOf each (5,6)
11
>>> sumOf folded [1,2,3,4]
10
>>> sumOf (folded % each) [(1,2),(3,4)]
10

sum ≡ sumOf folded

This operation may be more strict than you would expect. If you want a lazier version use \o -> getSum . foldMapOf o Sum

asumOf :: (Is k A_Fold, Alternative f) => Optic' k is s (f a) -> s -> f a

The sum of a collection of actions.

>>> asumOf each ("hello","world")
"helloworld"

>>> asumOf each (Nothing, Just "hello", Nothing)
Just "hello"

asum ≡ asumOf folded

msumOf :: (Is k A_Fold, MonadPlus m) => Optic' k is s (m a) -> s -> m a

The sum of a collection of actions.

>>> msumOf each ("hello","world")
"helloworld"

>>> msumOf each (Nothing, Just "hello", Nothing)
Just "hello"

msum ≡ msumOf folded

elemOf :: (Is k A_Fold, Eq a) => Optic' k is s a -> a -> s -> Bool

Does the element occur anywhere within a given Fold of the structure?

>>> elemOf each "hello" ("hello","world")
True

elem ≡ elemOf folded

notElemOf :: (Is k A_Fold, Eq a) => Optic' k is s a -> a -> s -> Bool

Does the element not occur anywhere within a given Fold of the structure?

>>> notElemOf each 'd' ('a','b','c')
True

>>> notElemOf each 'a' ('a','b','c')
False

notElem ≡ notElemOf folded

lengthOf :: Is k A_Fold => Optic' k is s a -> s -> Int

Calculate the number of targets there are for a Fold in a given container.

Note: This can be rather inefficient for large containers and just like length, this will not terminate for infinite folds.

length ≡ lengthOf folded

>>> lengthOf _1 ("hello",())
1

>>> lengthOf folded [1..10]
10

>>> lengthOf (folded % folded) [[1,2],[3,4],[5,6]]
6

maximumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a

Obtain the maximum element (if any) targeted by a Fold safely.

Note: maximumOf on a valid Iso, Lens or Getter will always return Just a value.

>>> maximumOf folded [1..10]
Just 10

>>> maximumOf folded []
Nothing

>>> maximumOf (folded % filtered even) [1,4,3,6,7,9,2]
Just 6

maximum ≡ fromMaybe (error "empty") . maximumOf folded

In the interest of efficiency, This operation has semantics more strict than strictly necessary. \o -> getMax . foldMapOf o Max has lazier semantics but could leak memory.

minimumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a

Obtain the minimum element (if any) targeted by a Fold safely.

Note: minimumOf on a valid Iso, Lens or Getter will always return Just a value.

>>> minimumOf folded [1..10]
Just 1

>>> minimumOf folded []
Nothing

>>> minimumOf (folded % filtered even) [1,4,3,6,7,9,2]
Just 2

minimum ≡ fromMaybe (error "empty") . minimumOf folded

In the interest of efficiency, This operation has semantics more strict than strictly necessary. \o -> getMin . foldMapOf o Min has lazier semantics but could leak memory.

maximumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a

Obtain the maximum element (if any) targeted by a Fold according to a user supplied Ordering.

>>> maximumByOf folded (compare `on` length) ["mustard","relish","ham"]
Just "mustard"

In the interest of efficiency, This operation has semantics more strict than strictly necessary.

maximumBy cmp ≡ fromMaybe (error "empty") . maximumByOf folded cmp

minimumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a

Obtain the minimum element (if any) targeted by a Fold according to a user supplied Ordering.

In the interest of efficiency, This operation has semantics more strict than strictly necessary.

>>> minimumByOf folded (compare `on` length) ["mustard","relish","ham"]
Just "ham"

minimumBy cmp ≡ fromMaybe (error "empty") . minimumByOf folded cmp

findOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Maybe a

The findOf function takes a Fold, a predicate and a structure and returns the leftmost element of the structure matching the predicate, or Nothing if there is no such element.

>>> findOf each even (1,3,4,6)
Just 4

>>> findOf folded even [1,3,5,7]
Nothing

find ≡ findOf folded

findMOf :: (Is k A_Fold, Monad m) => Optic' k is s a -> (a -> m Bool) -> s -> m (Maybe a)

The findMOf function takes a Fold, a monadic predicate and a structure and returns in the monad the leftmost element of the structure matching the predicate, or Nothing if there is no such element.

>>> findMOf each (\x -> print ("Checking " ++ show x) >> return (even x)) (1,3,4,6)
"Checking 1"
"Checking 3"
"Checking 4"
Just 4

>>> findMOf each (\x -> print ("Checking " ++ show x) >> return (even x)) (1,3,5,7)
"Checking 1"
"Checking 3"
"Checking 5"
"Checking 7"
Nothing

findMOf folded :: (Monad m, Foldable f) => (a -> m Bool) -> f a -> m (Maybe a)

lookupOf :: (Is k A_Fold, Eq a) => Optic' k is s (a, v) -> a -> s -> Maybe v

The lookupOf function takes a Fold, a key, and a structure containing key/value pairs. It returns the first value corresponding to the given key. This function generalizes lookup to work on an arbitrary Fold instead of lists.

>>> lookupOf folded 4 [(2, 'a'), (4, 'b'), (4, 'c')]
Just 'b'

>>> lookupOf folded 2 [(2, 'a'), (4, 'b'), (4, 'c')]
Just 'a'

Combinators

pre :: Is k A_Fold => Optic' k is s a -> AffineFold s a

Convert a fold to an AffineFold that visits the first element of the original fold.

For the traversal version see singular.

backwards_ :: Is k A_Fold => Optic' k is s a -> Fold s a

This allows you to traverse the elements of a Fold in the opposite order.

Monoid structures

Fold admits (at least) two monoid structures:

• summing concatenates results from both folds.
• failing returns results from the second fold only if the first returns no results.

In both cases, the identity element of the monoid is ignored, which returns no results.

There is no Semigroup or Monoid instance for Fold, because there is not a unique choice of monoid to use, and the (<>) operator could not be used to combine optics of different kinds. When porting code from lens that uses <> to combine folds, use summing instead.

summing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a infixr 6

Return entries of the first Fold, then the second one.

>>> toListOf (_1 % ix 0 `summing` _2 % ix 1) ([1,2], [4,7,1])
[1,7]

failing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a infixl 3

Try the first Fold. If it returns no entries, try the second one.

>>> toListOf (ix 1 `failing` ix 0) [4,7]
[7]
>>> toListOf (ix 1 `failing` ix 0) [4]
[4]

Subtyping

data A_Fold :: OpticKind

Tag for a fold.

Instances

Is An_AffineFold A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints An_AffineFold p -> r) -> Constraints A_Fold p -> r

Is A_Getter A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints A_Getter p -> r) -> Constraints A_Fold p -> r

Is A_ReversedPrism A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints A_ReversedPrism p -> r) -> Constraints A_Fold p -> r

Is A_Traversal A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints A_Traversal p -> r) -> Constraints A_Fold p -> r

Is An_AffineTraversal A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints An_AffineTraversal p -> r) -> Constraints A_Fold p -> r

Is A_Prism A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints A_Prism p -> r) -> Constraints A_Fold p -> r

Is A_Lens A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints A_Lens p -> r) -> Constraints A_Fold p -> r

Is An_Iso A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: (Constraints An_Iso p -> r) -> Constraints A_Fold p -> r

(s ~ t, a ~ b) => ToReadOnly A_Fold s t a b

Defined in Optics.ReadOnly

Methods

getting :: Optic A_Fold is s t a b -> Optic' (Join A_Getter A_Fold) is s a

(s ~ t, a ~ b) => IxOptic A_Fold s t a b

Defined in Optics.Indexed.Core

Methods

noIx :: NonEmptyIndices is => Optic A_Fold is s t a b -> Optic A_Fold NoIx s t a b