Optics.Prism

A Prism generalises the notion of a constructor (just as a Lens generalises the notion of a field).

Formation

type Prism s t a b = Optic A_Prism NoIx s t a b

Type synonym for a type-modifying prism.

type Prism' s a = Optic' A_Prism NoIx s a

Type synonym for a type-preserving prism.

Introduction

prism :: (b -> t) -> (s -> Either t a) -> Prism s t a b

Build a prism from a constructor and a matcher, which must respect the well-formedness laws.

If you want to build a Prism from the van Laarhoven representation, use prismVL from the optics-vl package.

Elimination

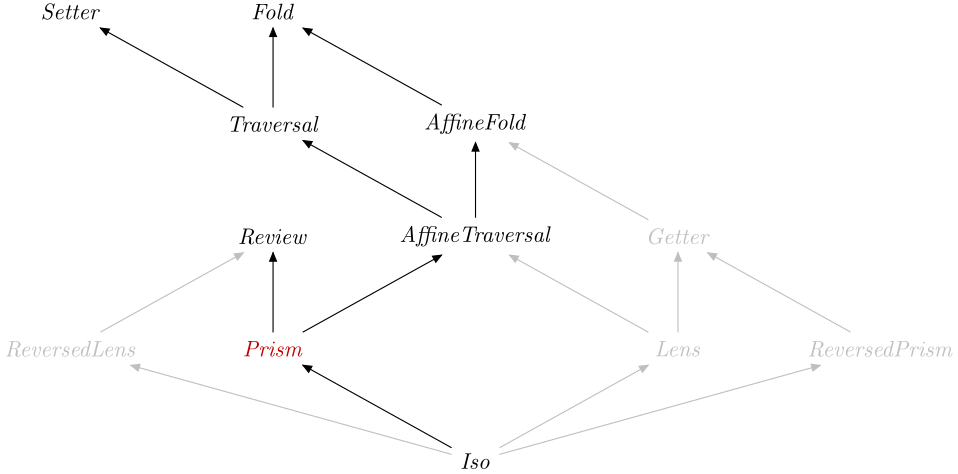
A Prism is in particular an AffineFold, a Review and a Setter, therefore you can specialise types to obtain:

preview :: Prism s t a b -> s -> Maybe a
review  :: Prism s t a b -> b -> t

over    :: Prism s t a b -> (a -> b) -> s -> t
set     :: Prism s t a b ->       b  -> s -> t

Computation

review   (prism f g) ≡ f
matching (prism f g) ≡ g

Well-formedness

matching o (review o b) ≡ Right b
matching o s ≡ Right a  =>  review o a ≡ s

Additional introduction forms

See Data.Maybe.Optics and Data.Either.Optics for Prisms for the corresponding types, and _Cons, _Snoc and _Empty for Prisms for container types.

prism' :: (b -> s) -> (s -> Maybe a) -> Prism s s a b

This is usually used to build a Prism', when you have to use an operation like cast which already returns a Maybe.

only :: Eq a => a -> Prism' a ()

This Prism compares for exact equality with a given value.

>>> only 4 # ()
4

>>> 5 ^? only 4
Nothing

nearly :: a -> (a -> Bool) -> Prism' a ()

This Prism compares for approximate equality with a given value and a predicate for testing, an example where the value is the empty list and the predicate checks that a list is empty (same as _Empty with the AsEmpty list instance):

>>> nearly [] null # ()
[]
>>> [1,2,3,4] ^? nearly [] null
Nothing

nearly [] null :: Prism' [a] ()

To comply with the Prism laws the arguments you supply to nearly a p are somewhat constrained.

We assume p x holds iff x ≡ a. Under that assumption then this is a valid Prism.

This is useful when working with a type where you can test equality for only a subset of its values, and the prism selects such a value.

Additional elimination forms

withPrism :: Is k A_Prism => Optic k is s t a b -> ((b -> t) -> (s -> Either t a) -> r) -> r

Work with a Prism as a constructor and a matcher.

Combinators

aside :: Is k A_Prism => Optic k is s t a b -> Prism (e, s) (e, t) (e, a) (e, b)

Use a Prism to work over part of a structure.

without :: (Is k A_Prism, Is l A_Prism) => Optic k is s t a b -> Optic l is u v c d -> Prism (Either s u) (Either t v) (Either a c) (Either b d)

Given a pair of prisms, project sums.

Viewing a Prism as a co-Lens, this combinator can be seen to be dual to alongside.

below :: (Is k A_Prism, Traversable f) => Optic' k is s a -> Prism' (f s) (f a)

Lift a Prism through a Traversable functor, giving a Prism that matches only if all the elements of the container match the Prism.

Subtyping

data A_Prism

Tag for a prism.

Instances

ReversibleOptic A_Prism

Defined in Optics.Re

Associated Types

type ReversedOptic A_Prism = (r :: Type)

Methods

re :: AcceptsEmptyIndices "re" is => Optic A_Prism is s t a b -> Optic (ReversedOptic A_Prism) is b a t s

Is A_Prism A_Review

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism A_Review p -> (Constraints A_Prism p -> r) -> Constraints A_Review p -> r

Is A_Prism A_Fold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism A_Fold p -> (Constraints A_Prism p -> r) -> Constraints A_Fold p -> r

Is A_Prism An_AffineFold

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism An_AffineFold p -> (Constraints A_Prism p -> r) -> Constraints An_AffineFold p -> r

Is A_Prism A_Setter

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism A_Setter p -> (Constraints A_Prism p -> r) -> Constraints A_Setter p -> r

Is A_Prism A_Traversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism A_Traversal p -> (Constraints A_Prism p -> r) -> Constraints A_Traversal p -> r

Is A_Prism An_AffineTraversal

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy A_Prism An_AffineTraversal p -> (Constraints A_Prism p -> r) -> Constraints An_AffineTraversal p -> r

Is An_Iso A_Prism

Defined in Optics.Internal.Optic.Subtyping

Methods

implies :: proxy An_Iso A_Prism p -> (Constraints An_Iso p -> r) -> Constraints A_Prism p -> r

ArrowChoice arr => ArrowOptic A_Prism arr

Defined in Optics.Arrow

Methods

overA :: Optic A_Prism is s t a b -> arr a b -> arr s t

ToReadOnly A_Prism s t a b

Defined in Optics.ReadOnly

Methods

getting :: Optic A_Prism is s t a b -> Optic' (Join A_Getter A_Prism) is s a

type ReversedOptic A_Prism

Defined in Optics.Re

type ReversedOptic A_Prism = A_ReversedPrism